How To Find The Variables In A Word Problem Money
Money Word Problems
The hush-hush to success in solving coin word problems is to exist able to set up the right systems of equations and precisely solve it using the commutation method or at times, the elimination method.
It'south besides worth pointing out that the presentation of the algebraic expressions in money word problems are a bit different and not so straightforward compared to what we're used to. For example, instead of proverb "the number of nickels is ii more than the number of dimes", you'll often see this expressed in coin word bug every bit "there are ii more than nickels than dimes". Both algebraic expressions tin can exist written in an equation every bit n=d+2 merely just expressed differently.
Therefore, it is crucial to have a smashing eye and agreement of the information given in a money word problem so we can translate the algebraic expressions correctly into equations. More than importantly, yous must exist familiar with the value of each kind of Us coin.
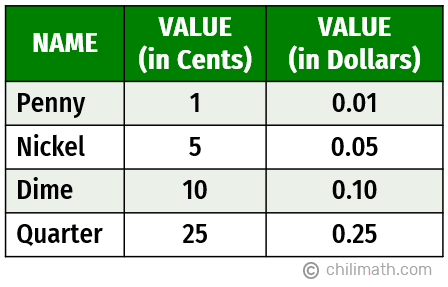
Notation: In solving our bug below, nosotros will use the value of the coins in dollars which are listed nether the third column in the table above. As you lot tin meet, the penny has a value of 0.01, the nickel has a value of 0.05, the dime has a value of 0.x, and the quarter has a value of 0.25.
Example 1: Tamara has 35 coins in nickels and quarters. In all, she has $4.15. How many of each kind of money does she take?
Right off the bat, the problem gives us two important pieces of information. Outset, information technology tells us that in that location is a total number of 35 coins consisting of nickels and quarters. Secondly, the total value of the coins is $4.15. We need to translate these statements into algebraic equations to discover how many nickels and how many quarters she has.
Money word issues ordinarily involve 2 types of equations. One equation describes the full number of coins while the other describes the total amount of money.
But before we start writing our equations, allow's select variables that will stand for the unknown values in our problem.
- Let due north = number of nickels
- Permit q = number of quarters
At present that we have our variables, permit'southward write the ii statements into equations.
1) Tamara has 35 coins in nickels and quarters.
Equation #1: due north + q = 35
ii) In all, she has $4.15.
Equation #2: 0.05n + 0.25q = iv.15
Note that in Equation #2, we multiplied the value of each money (in dollars) by how many of that specific coin we take. So, since nickel is worth 5 cents, we multiplied 0.05 by the number of nickels (north) and multiplied 0.25 by the number of quarters (q) since a quarter is worth 25 cents. We added both algebraic expressions and ready information technology equal to the total value of the coins.
This setup, however, results in Equation #2 having two variables. So to solve for the full corporeality of money, we get-go need to define one of the coins in terms of the other. In other words, we need to limited the number of nickels in terms of the number of quarters or vice versa.
From Equation #1, if we subtract the number of quarters from 35 (which is the total number of coins), what nosotros'll get is the number of nickels. We tin write this algebraically as,
n = 35 - q
By doing this, we now have our number of nickels (n) defined in terms of the number of quarters (q).
Our next stride is to substitute the expression for n into Equation #two and solve for the number of quarters (q). By defining n in terms of q, we now accept an equation with only one variable.
Solution:

Perfect! This tells united states of america that the number of quarters is 12. Since the problem is asking us to find how many of each coin Tamara has, we volition only decrease 12 from 35 to get the number of nickels.
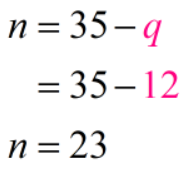
And so we have,
- Number of Nickels: 23
- Number of Quarters: 12
Respond: Tamara has 23 nickels and 12 quarters.
Check:
When solving word issues, it's of import to always verify if you got the correct answers. To check, nosotros can plug in the values that we got for due north and q into Equation #2 and see if both sides of the equation equal each other.
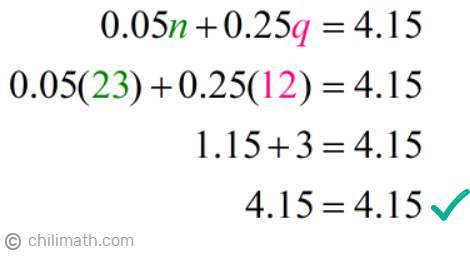
Note that you may also use Equation #ane to bank check your answers. Like what nosotros only did, y'all merely have to substitute n and q with 23 and 12, respectively, and see if they equal 35 which is the total number of coins.
Instance two: My brother has been putting just nickels and dimes in his piggy banking company. He is able to salve up to $3.65. If he has 4 more than nickels than dimes, how many of each kind of coin does my brother have?
Let's start by picking our variables that volition correspond the number of each type of coin.
- Let n = number of nickels
- Let d = number of dimes
In this example, we don't know how many coins at that place are in full. Withal, we know that the coins inside the piggy bank only consist of nickels and dimes which amount to $3.65. Translating this into an algebraic equation, we can write this as
Equation #1: 0.05n + 0.10d = 3.65
We are also told that there are 4 more nickels than dimes which means that the number of nickels (north) is equal to the number of dimes (d) plus 4 more.
Equation #two: due north = d+4
Every bit you can see in Equation #two, we already have the nickels (n) defined in terms of the dimes (d). In this case, we can go ahead and substitute northward with d + 4 in Equation #1, then solve for d.
Solution:

So, this ways that at that place are 23 dimes. Since at that place are 4 more than nickels than dimes, and so there must be 27 nickels. We also get in at the same reply when solving for north using Equation #2.
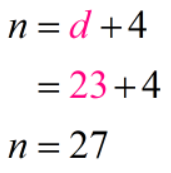
Going back to our original problem, how many of each kind of coin does my brother have?
Answer: My brother has 27 nickels and 23 dimes.
Check:
Permit'south plug in the values that we got for n and d into Equation #1 to see if they corporeality to the total value of the coins which is $3.65.

Example 3: A jar of coins has one-third as many dimes as quarters. If the total amount of coins is $5.10, how many dimes and quarters are in the jar?
Before we translate the important statements that are provided in the problem, let's kickoff select the variables for the unknown values.
- Let d = number of dimes
- Let q = number of quarters
1) A jar of coins has one-third equally many dimes every bit quarters
Equation #1: \large{d = {ane \over 3}q}
two) The total amount of coins is $5.10
Equation #2: 0.10d + 0.25q = five.ten
This problem involves a fraction only the setup is the aforementioned every bit our previous instance. Over again, we are non given the total number of coins, but nosotros are told that the total value of the dimes and quarters is $5.x.
We were already able to define the number of dimes (d) in terms of the number of quarters (q) in Equation #1. So in solving for q using Equation #2, we will merely substitute d with the expression \big{1 \over 3}q
Solution:
![0.10[(1/3)q]+0.25q=5.10 → q=18](https://www.chilimath.com/wp-content/uploads/2020/12/ex3_solution.png)
And so at that place are 18 quarters. Let's now use this value to detect the number of dimes.
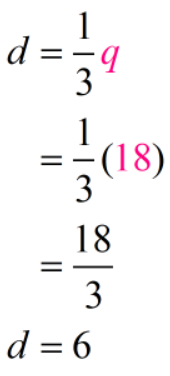
Therefore, we have
- Number of Dimes: 6
- Number of Quarters: 18
Answer: At that place are 6 dimes and eighteen quarters in the jar.
Check:
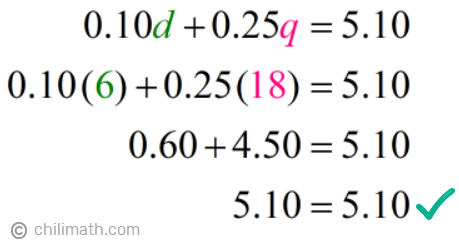
Example four: Damian had two-thirds equally many pennies equally nickels. The full value of his coins was $2.38. Observe the number he had of each kind of money.
This problem is quite similar to Example 3 and so y'all should exist familiar already with the steps needed to answer this word trouble.
- Let p = number of pennies
- Let north = number of nickels
What pieces of information are given to u.s.?
1) Damian had two-thirds every bit many pennies as nickels.
Equation #1: \large{p = {two \over three}northward}
two) The full value of his coins was $2.38.
Equation #2: 0.01p + 0.05n = 2.38
Let's now substitute the expression of p in Equation #2 and solve for n.
Solution:
![0.01[(2/3)n]+0.15n=2.38 → n=42](https://www.chilimath.com/wp-content/uploads/2020/12/ex4_solution.png)
Now that we know how many nickels there are, let'southward motility on and find the number of pennies also.
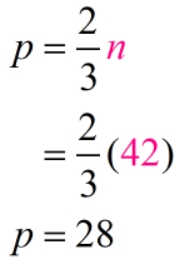
We got the following values:
- Number of Pennies: 28
- Number of Nickels: 42
Respond: Damian had 28 pennies and 42 nickels.
Check:
This time, I'll leave information technology up to you to cheque if both of the values we got for the number of pennies and the number of nickels are correct. You may substitute p and northward in Equation #2 with the values and verify if indeed the amount of both coins when added, equals to $2.38.
Example 5: Aunt Sheila has $2.50 in nickels and dimes in her wallet. How many of each kind of money does she have, if the number of dimes exceeds twice the number of nickels by 5?
Nosotros'll first pick our variables to stand for the nickels and dimes, and so examine the important details given to usa in the problem.
- Permit north = number of nickels
- Let d = number of dimes
Let's interpret each statement algebraically into an equation.
i) Aunt Sheila has $ii.l in nickels and dimes in her wallet.
Equation #ane: 0.05n + 0.10d = 2.50
ii) The number of dimes exceeds twice the number of nickels past 5.
Equation #2: d=2n+v
Since the number of dimes (d) is already expressed in terms of the number of nickels, we tin can continue in solving for n using Equation #i.
Solution:

This tells united states of america that at that place are 8 nickels. Since it says that the number of dimes is v more than than twice the number of nickels, then let'due south use Equation #two to find how many dimes Aunt Shiela has.
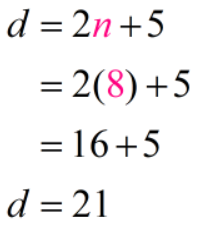
Reply: Aunt Shiela has 8 nickels and 21 dimes.
Check:
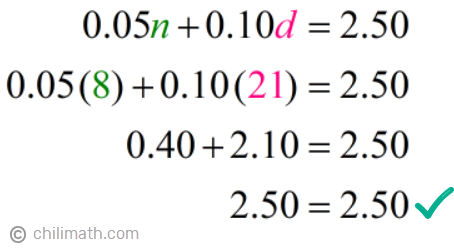
Example vi: I found coins worth $vi.97 in my Grandpa'south drawer. Surprisingly, the number of pennies, nickels, dimes, and quarters are all the same. How many of each kind of coin did I observe?
This problem is quite unique as it involves not merely two simply four kinds of coins. Since the quantity for each money is the aforementioned equally the other coins, we will select but ane variable to stand for each kind. Let's selection "c".
- Permit c = number of pennies
- Let c = number of nickels
- Permit c = number of dimes
- Let c = number of quarters
At present that we have our variable, let'due south examine the information given to us closely. Nosotros are told that the coins amount to $6.97. Since the quantity for each type of money (c) is the aforementioned as the others, we will multiply the value of each coin in dollars with c, add all values of the coins together then ready it equal to the total value of all the coins which is $6.97. Therefore, we take
Equation: 0.01c + 0.05c + 0.10c + 0.25c = 6.97
We have covered all the of import details from our problem in the equation in a higher place so we tin go ahead and proceed to solve for c.
Solution:

Nifty! We now know that there are 17 coins for each type of coin.
Answer: There are 17 pennies, 17 nickels, 17 dimes, and 17 quarters in my Grandpa's drawer.
Check:
The last thing that we need to do is to verify that all the coins indeed amount to $half dozen.97.

Example 7: Mrs. Potter received $3.44 of modify after paying for her groceries. The cashier gave her a total of 47 coins in pennies, nickels, and dimes. If she received the same number of pennies and nickels, how many of each money did she receive?
Here nosotros accept a coin give-and-take trouble that is packed with information – which is good! The more details are provided to us, the amend. ???? As you lot can see, we are given the total value of the coins, the total number of coins, and the kinds of coins.
Since Mrs. Potter received the same quantity of pennies and nickels merely a dissimilar quantity of dimes; we'll use the variable c to stand up for the number of pennies and nickels, and the variable d to correspond the number of dimes.
- Let c = number of pennies
- Allow c = number of nickels
- Let d = number of dimes
If you lot oasis't realized still, this problem is quite unique merely like our previous example. It involves three types of coins but we're only using two variables to represent them due to the same number of pennies and nickels.
Beginning, we're told that Mrs. Potter received $3.44 in pennies, nickels, and dimes. To translate this statement into an algebraic equation, information technology just makes sense to add together the values for each blazon of coin together so set it equal to $3.44.
Equation #i: 0.01c + 0.05c + 0.10d = 3.44
Side by side, it says that the cashier gave her a total of 47 coins in pennies, nickels, and dimes. This 1 is easier to translate into an equation since nosotros just have to add the number of pennies, nickels, and dimes on the left-hand side of the equation then set it equal to 47.
Equation #2: c + c + d = 47
At this betoken, Equation #1 still has two variables. So before we can go along to find how many of each type of coin she received, we need to express the number of dimes (d) in terms of the number of pennies and nickels (c) first. Nosotros tin practise this by solving for (d) using Equation #2.
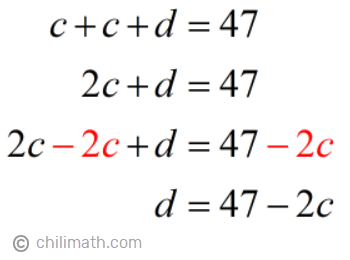
We'll substitute the value of d with 47 - 2c in Equation #i then solve for c. In doing so, we will only be working with one variable.
Solution:

Perfect! This tells us that there were nine pennies and 9 nickels. So at present, all we have left to do is to detect how many dimes there were. We already had the equation for d which is d = 47 - 2c. Using the value we got for c, we have
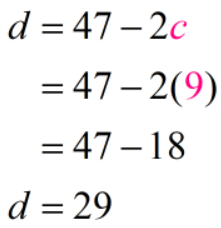
Let'due south recap:
- Number of Pennies: nine
- Number of Nickels: 9
- Number of Dimes: 29
Answer: Mrs. Potter received nine pennies, 9 nickels, and 29 dimes.
Check:
Let's verify our answers rapidly by plugging the values of c and d, into Equation #2:
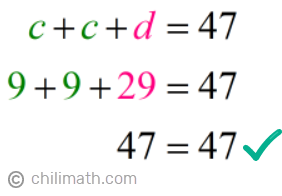
Another option too is to do your check using Equation #1.
Instance 8: Mom gave the pizza delivery guy $7.88 in pennies, dimes, and quarters every bit a tip. She gave him 12 more quarters than pennies and 8 more dimes than quarters. Find the number of each kind of coin that she gave as a tip.
This last example is also an interesting one. Right away, we tin see that we are given the total value of the coins and that the tip consists of 3 types of coins. The quarters are also defined in terms of the pennies while the dimes are described in terms of the quarters.
Just like in our previous examples, let'due south start past selecting variables to stand up for each blazon of coin.
- Let p = number of pennies
- Let d = number of dimes
- Permit q = number of quarters
Now let's examine and translate each statement algebraically into an equation that we can solve.
1) Mom gave the pizza commitment guy $7.88 in pennies, dimes, and quarters as a tip.
Equation #1: 0.01p + 0.10d + 0.25q = vii.88
two) She gave him 12 more quarters than pennies and 8 more than dimes than quarters.
Nosotros can translate this statement into two equations to show the number of quarters defined in terms of the number of pennies and the number of dimes defined in terms of the number of quarters.
Equation #2: q = p + 12
Equation #3: d = q + 8
At this fourth dimension, the pennies are not defined in terms of any of the 2 coins. But since the dimes are already described in terms of the quarters and the quarters are described in terms of the pennies, it merely makes sense for us to describe the number of pennies in terms of the number of quarters also. We can do this using Equation #two.
q = p + 12 → \color{ruby}p = q - 12
In doing so, both the number of dimes and pennies are divers in terms of q making it possible for the states to solve Equation #one with simply i variable. In other words, we volition substitute p and d in Equation #1 with their respective algebraic expressions then solve for q.
Solution:

Excellent! This tells us that there were 20 quarters. But since our original problem asks us to discover the number for each type of money, let's as well notice out how many pennies and dimes were at that place, past plugging in the value of the number of quarters into Equation #3 and in the equation for the number of pennies (p).
- Number of Pennies:
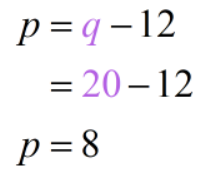
- Number of Dimes:
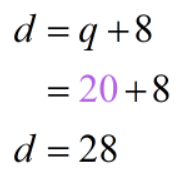
Answer: Mom gave 8 pennies, 28 dimes, and 20 quarters equally a tip.
Check:

Source: https://www.chilimath.com/lessons/algebra-word-problems/coin-word-problems/
Posted by: jentforely.blogspot.com

0 Response to "How To Find The Variables In A Word Problem Money"
Post a Comment